Este rompecabezas está basado en el skewb, habiéndose modificado las piezas para darle forma esférica. Las esquinas del skewb se han transformado en triángulos de un solo color y los centros conservan su forma cuadrada. Como en el skewb, hay cuatro planos de giro y cada movimiento rota 120 grados la mitad del puzzle (que en este caso conserva en todo momento su forma).

La bola está coloreada como el típico balón de playa, con cuatro sectores a modo de rodajas: dos más estrechos, azul y verde; y dos más anchos, amarillo y rojo. Los sectores estrechos están formados por dos triángulos y un cuadrado; los más anchos, por dos triángulos y dos cuadrados. Ambos tipos de sectores se alternan.
En la actualidad parece ser un puzzle difícil de encontrar.
En el sitio web de James Storer se puede encontrar una patente de Uwe Meffert de 1994 de un juguete denominado Puzzle Ball. Esta patente cubre puzzles con forma de bola basados en el skewb y comercializados por Meffert con distintos nombres, como Creative Puzzle Ball, Mickey Challenge o este Beach Puzzle Ball. Pero en la página de Storer aparecen fotos de puzzles húngaros similares muy anteriores (de 1980).
El Beach Puzzle Ball tiene solo 2160 estados posibles, un número muy bajo para este tipo de puzzles. El análisis por ordenador ha demostrado que todas esas posiciones son alcanzables en no más de 6 movimientos. Estos datos han sido tomados de la página de Jaap Scherphuis.
El Beach Puzzle Ball es un skewb simplificado, por tanto es más fácil que éste. En la página de Meffert no aparece asignada dificultad para este rompecabezas, pero sí para el skewb normal, con dificultad 2 (entre 1 y 6).
Usaremos una notación mixta, que dependerá de la fase de resolución. En cada caso colocaremos la esfera de una forma.

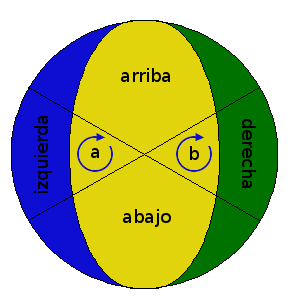
En el primer caso pondremos ante nosotros uno de los segmentos estrechos y moveremos las semiesferas derecha (movimiento d) o izquierda (movimiento i) indicadas en el dibujo 1. En el segundo caso tendremos dos piezas triangulares a izquierda y derecha como se ve en el dibujo 2 y giraremos la semiesfera que tiene en el centro uno de los triángulos. Son los movimientos a y b. Los movimientos inversos serán i', d', a' y b'.
La solución se basa principalmente en la secuencia ab'a'b, que intercambia los cuadrados arriba-abajo y derecha-izquierda. La hemos dividido en cuatro fases, pero todas ellas son cortas y sencillas.

Completamos un segmento estrecho, verde o azul. Es casi seguro que al menos uno de ellos esté a medio hacer, con un triángulo ya junto al cuadrado de su color. En cualquier caso, en no más de dos movimientos habremos conseguido este primer objetivo.
Colocamos el segmento en vertical y miramos los triángulos a izquierda y derecha del cuadrado. Uno (no importa cual) debe ser rojo y el otro amarillo. Si no es así bastará ejecutar i/i' (uno de los dos) y/o d/d' (uno de los dos).
El triángulo que está a la izquierda del triángulo izquierdo debe ser del mismo color que éste. Igualmente el triángulo que está a la derecha del triángulo derecho debe ser de su mismo color. Si no es este el caso, colocamos la esfera con la rodaja ya hecha en posición horizontal y ejecutamos did.
A continuación vamos a completar la otra rodaja fina (azul en la siguiente figura). Los triángulos ya están colocados, pero es posible que el cuadrado no. Ponemos la bola de forma que el cuadrado a colocar esté arriba y ejecutamos aba'b'.

Quedan por completar los segmentos anchos, amarillo y rojo. Los triángulos están ya bien colocados, así que además de la posición ordenada final (que también puede darse casualmente), hay dos posibilidades: que haya un cuadrado rojo en la zona amarilla y un cuadrado amarillo en la zona roja (es lo más habitual); o que los dos cuadrados rojos estén en la zona amarilla y los dos cuadrados amarillos en la zona roja.
El primer caso tiene a su vez dos subcasos: que los cuadrados intrusos sean opuestos o adyacentes.
Si están en posiciones opuestas, ponemos la bola con uno de los segmentos anchos en posición vertical y ejecutamos ab'a'b. Después de esto tendremos a los dos cuadrados rojo y amarillo intrusos en posiciones vecinas y a los cuadrados azul y verde intercambiados (dibujo siguiente).

Si están en posiciones adyacentes, las intercambiamos como en el caso anterior, poniendo uno arriba y otro abajo (dibujo siguiente) y ejecutando ab'a'b.
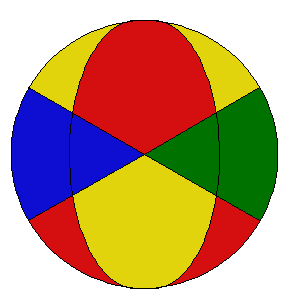
En el segundo caso ponemos el puzzle de forma que arriba haya un cuadrado amarillo y abajo un cuadrado rojo o al revés, y ejecutamos ab'a'b. Tendremos un cuadrado rojo en la zona amarilla y un cuadrado amarillo en la zona roja, ambos vecinos; además, los cuadrados azul y verde estarán intercambiados. Poniendo los cuadrados amarillo y rojo intrusos arriba y abajo (no importa cuál arriba y cuál abajo) y ejecutando ab'a'b se terminará de ordenar el puzzle.
Rodolfo Valeiras Reina, 1 de junio de 2013.