El skewb es un rompecabezas del tipo del cubo de Rubik. Como éste, también consiste en un cubo compuesto por piezas que pueden cambiar de posición. Al principio, cada cara del cubo es de un color uniforme; cuando se han realizado algunos movimientos al azar, los colores se mezclan. Por supuesto, el objetivo es volver a poner el cubo en su estado original.

Mientras que el cubo de Rubik está cortado por seis planos paralelos a las caras, el skewb está cortado por sólo cuatro planos, perpendiculares a las diagonales. Cada uno de estos planos divide al cubo en dos partes iguales. Un movimiento consiste en rotar 120 grados cualquiera de estos semicubos.


El skewb está formado por dos clases de piezas: ocho esquinas, con tres colores cada una; y seis centros monocromos de forma cuadrada. Cada movimiento desplaza cuatro esquinas y tres centros.
El skewb es un rompecabezas antiguo, sólo un poco posterior al cubo de Rubik. Fue inventado por el periodista inglés Tony Durham y comercializado por Uwe Meffert, al principio con el nombre de Pyraminx Cube. Después le cambió el nombre de acuerdo con la opinión manifestada por Douglas Hofstadter en su sección de Temas Matemágicos de la revista Investigación y Ciencia (julio de 1982 en la versión original). Este nombre es una mezcla entre skew (torcer) y cube (cubo).
El skewb tiene 3.149.280 estados posibles (el cubo de Rubik tiene más de 4×1019). Mediante un análisis computerizado exhaustivo se ha comprobado que todas las posiciones se pueden resolver en 11 o menos movimientos (véase 2).
Está montado sobre una estructura parecida a la del cubo de Rubik, pero en este caso, del centro no salen seis ramas, sino cuatro, que terminan en sendas cuatro esquinas (formando un tetraedro regular).

Estas esquinas, por tanto, son fijas, aunque pueden girar sobre sí mismas. Las demás piezas se sujetan a estas piezas básicas mediante lengüetas.
Dentro de este tipo de rompecabezas, skewb es considerado de dificultad media-baja. Meffert le asigna dificultad 2 (entre 1 y 6).
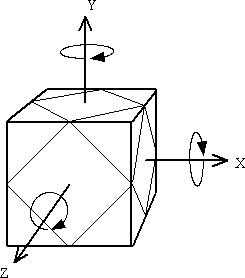
Hay ocho movimientos posibles (uno por cada vértice) y sus opuestos. Fijada una posición para el cubo, sus vértices y los correspondientes movimientos serán designados de acuerdo con la siguiente convención:

Los movimientos en sentido horario se designarán con la letra minúscula correspondiente al vértice, mientras que los movimientos en sentido antihorario llevarán el superíndice -1. Por ejemplo, el movimiento a es un giro en sentido horario en torno al eje que va del vértice A al vértice G y llevará la pieza del vértice E al vértice B, la de B al D y la del D al E. Podemos resumir esto con la notación (E B D). La pieza del vértice A la dejará en el mismo sitio aunque con otra orientación. El movimiento a-1 tendrá el efecto (D B E).

Otros movimientos que usaremos a menudo serán b y b-1.

Los efectos sobre las piezas de las esquinas de los 16 movimientos simples son:
También se puede girar todo el cubo en torno a los ejes X, Y y Z. Estos giros se indicarán con la letra del eje y no se cuentan como movimientos. Como antes, consideraré positivos (X, Y, Z) los giros en sentido horario y negativos (X-1, Y-1, Z-1) los giros en sentido antihorario.
El método de resolución que se explica a continuación es sencillo y fácil de aprender, aunque está poco optimizado en cuanto al número de movimientos que requiere, que según mis cálculos puede llegar a 46 (aunque la mayoría de veces requiere menos de 30). Quien prefiera un método más corto puede consultar el enlace 2.
La base del método consiste en la secuencia ab-1a-1b. Su efecto es el siguiente:
Si repetimos la secuencia tres veces, el efecto sobre las esquinas superiores se anula, pero no la de los centros. Más interesante aún, si la ejecutamos dos veces, pero rotando 180 grados el cubo por el eje Y entre ambas ejecuciones, (ab-1a-1b Y2)2, el efecto sobre las esquinas también se anula, pero el efecto final sobre los centros es un 3-ciclo: atrás -> arriba -> frente.
Se elige una pieza-centro y se colocan a su lado las cuatro piezas-esquina. No hay que fijarse sólo en los colores de la cara donde está la pieza-centro, sino también en los de las caras contiguas. Esta parte es lo suficientemente sencilla para que todo el mundo pueda aprender a hacerla por sí solo, así que el lector debería pasar directamente a la segunda fase. Curiosamente, aunque es la parte más sencilla de la solución, es la más difícil de explicar, de ahí el espacio que le he tenido que dedicar. Pondremos la pieza-centro elegida (azul, por ejemplo) en la cara de arriba.
Supongamos que no hay ninguna esquina bien colocada. Si hay una pieza-esquina con la cara azul en la parte baja de una de las caras verticales del cubo, la ponemos frente a nosotros, como en el siguiente dibujo. Las zonas grises son de cualquier color (las de arriba, no azules).
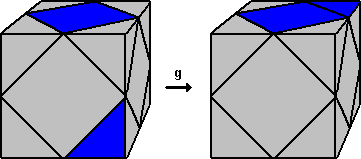
Para llevar arriba la pieza-esquina basta un movimiento, que en nuestra notación es g. Si la parte azul queda a la izquierda, el movimiento es h-1.

Si no hay ninguna pieza-esquina con la cara azul en la parte baja de una de las caras verticales del cubo, se puede llevar cualquiera a esta posición con un solo movimiento. Así que, como mucho, en dos movimientos estará colocada la primera esquina.
Una vez colocada la primera pieza-esquina, queda perfectamente determinada la posición para las demás. Por ejemplo, si hemos colocado la pieza azul-amarilla-blanca en la posición de la figura, a su izquierda debe colocarse la otra esquina azul-amarilla (azul-amarilla-roja). Esta pieza sólo se puede encontrar en una de las posiciones marcadas de gris oscuro en el siguiente dibujo, más la esquina opuesta a la azul-amarilla-blanca (no visible). Esto se debe a que los movimientos del skweb no permiten trasladar una pieza-esquina a un vértice contiguo.

Si la pieza en cuestión (azul-amarilla-roja) se encuentra en el vértice trasero inferior izquierdo (H), se puede colocar en solo uno o dos movimientos. Si la cara azul está en la cara posterior del cubo, basta el movimiento d.

Si la cara azul está en otra posición, se puede poner en la cara trasera del cubo con uno de los movimientos h o h-1, que no afectan a las piezas ya colocadas. Si la pieza azul-amarilla-roja está en otro de los vértices, se puede trasladar a H con un solo movimiento, también sin afectar a las piezas colocadas. Así que se puede colocar la segunda pieza-esquina en un máximo de tres movimientos.
Ponemos el cubo de forma que queden las dos esquinas ya bien colocadas en la parte trasera. En el ejemplo, la pieza-esquina del vértice B (según la nueva posición del cubo) debe tener los colores azul, rojo y naranja. Esta pieza puede estar en tres posiciones, que aparecen marcadas de gris oscuro en la figura.

Si la pieza está en el vértice de la izquierda (D) y con la cara azul en la cara izquierda del cubo, basta un solo movimiento para colocarla.

Si la cara azul no está en esa posición hay que realizar un movimiento adicional (d o d-1) que no afecta a las piezas ya colocadas. Si la pieza está en cualquiera de las otras dos posiciones posibles se puede poner en el vértice D con otro movimiento (c o c-1), también sin afectar a las otras piezas. Por tanto, se puede colocar la tercera esquina en no más de tres movimientos.
Esta es la única de las piezas que plantea alguna dificultad. Puede estar en las posiciones marcadas de gris oscuro.

Si la pieza está en el vértice de la derecha (C) y con la cara azul en la cara derecha del cubo, basta un solo movimiento para colocarla.

Lo mismo pasa si la pieza está en el vértice H y con la cara azul en la cara trasera del cubo.

Si la pieza está en el vértice C, pero con la cara azul en la cara frontal del cubo, o en el vértice H, pero con la cara azul en la cara izquierda, hay que realizar un movimiento previo para ponerla donde queremos, pero este movimiento sí modifica la posición de una de las esquinas ya colocadas, que habrá que recolocar después.
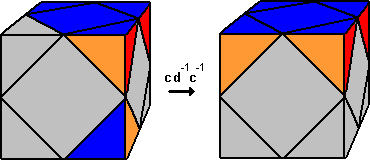

Si la pieza está en C o en H con la cara azul en la base del cubo se debe hacer un movimiento (d o d-1 respectivamente) para ponerla en una cara lateral. Si está en A (mal orientado, se entiende) se debe mover también d o d-1 para ponerlo en C o H con la cara azul en una cara lateral del cubo. Esto hace un máximo de cuatro movimientos para colocar la cuarta pieza-esquina, y un total de 12 movimientos (como máximo) para esta primera fase.
Una vez terminada la primera fase, las cuatro piezas esquina restantes estarán en sus posiciones correctas (el skewb es así de amable), si bien normalmente no bien orientadas. Le daremos la vuelta al cubo y miraremos dónde se encuentran los cuatro triángulos del color de la cara superior. Podemos identificar este color (verde en el ejemplo) porque es el único que comparten las cuatro piezas-esquina. Realmente hay sólo dos posibilidades (además de la posición ordenada), que podemos representar con los siguientes esquemas.

Se trata de una vista desde arriba, con las caras laterales de las piezas-esquina desplegadas. Rotando el cubo por el eje Y siempre es posible ponerlo en una de estas situaciones. En el segundo caso se ejecuta la secuencia ab-1a-1b. En el primero, haremos antes ab-1a-1b Y-1, que nos lleva a la otra situación. Así pues, esta segunda fase tiene una longitud máxima de 8 movimientos.
Ya hay un centro bien colocado (azul, en el ejemplo), los demás pueden estar todos mal. En concreto puede haber mal colocados 3, 4 o 5 centros (o ninguno si ha habido mucha suerte). No puede haber dos centros mal colocados, porque eso implicaría una permutación impar sobre los centros, y cada movimiento simple del skewb supone un 3-ciclo sobre los centros, una permutación par.
Hay dos casos, según las caras donde se encuentran compartan o no un vértice. Lo podemos representar con el desarrollo plano del cubo (las caras grises son las que tienen mal el centro).

Necesariamente los centros deben estar desplazados por un 3-ciclo, y los casos posibles son los siguientes.
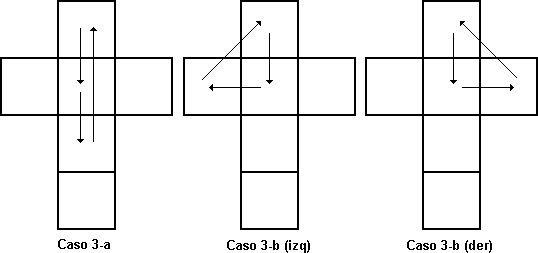
En cualquier caso, ponemos el cubo de forma que la pieza-centro que debe ir a la cara del frente se encuentre arriba. Si el otro centro mal colocado está atrás (caso 3-a) ejecutamos la secuencia (ab-1a-1b Y2)2. Si está a la izquierda (3-b izq) ejecutamos e-1 (Y2 ab-1a-1b)2 e. Si está a la derecha (3-b der) ejecutamos f (Y2 ab-1a-1b)2 f-1. Así que las dos variantes del caso 3-b se reducen al 3-a con un movimiento de ajuste anterior y posterior.
Orientamos el cubo poniendo abajo la cara ya terminada. Hay dos posibilidades: que todos los centros mal colocados estén en caras laterales o que uno de los centros mal colocados esté arriba.

En ninguno de los dos casos, los centros pueden estar formando un 4-ciclo (que sería una permutación impar), así que deben estar intercambiados por parejas. El caso 4-a se puede dividir en dos sub-casos según las piezas que hay que intercambiar estén juntas o enfrentadas.

Poniendo el cubo en cualquier posición de forma que las caras mal colocadas sean la del frente, la de arriba, la de atrás y la de abajo y efectuando la secuencia 3-ciclo que vimos antes, (ab-1a-1b Y2)2, pondremos el cubo en el caso 3-a. Otra posibilidad un poco más corta (dos movimientos) es poner una de las dos caras terminadas al frente y ejecutar, en el caso 4-a-1, con los centros a intercambiar arriba y a la izquierda y abajo y a la derecha, d-1 (aba-1b-1)3 d , y en el caso 4-a-2, d-1 (b-1a-1ba)3 d. Estamos reduciendo la situación al caso 4-b-2 que se verá ahora.
También el caso 4-b se divide en dos sub-casos, según haya o no alguna pareja enfrentada. El segundo tiene dos variantes simétricas.
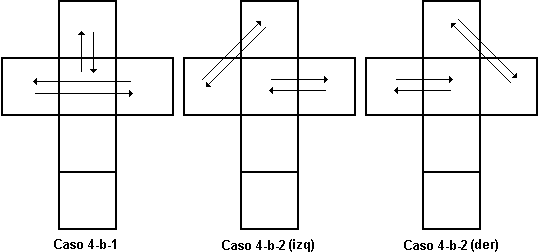
Para resolver el caso 4-b-1 se coloca el cubo de forma que las parejas de centros intercambiados estén arriba y al frente y a izquierda y derecha y se hace (ab-1a-1b)3. Para la versión izquierda del 4-b-2 las parejas serán arriba-izquierda y frente-derecha y se resuelve con (aba-1b-1)3. Para la versión derecha las parejas serán arriba-derecha y frente-izquierda y la secuencia es (b-1a-1ba)3.
Ponemos el cubo de forma que el centro que esté arriba deba ir al frente y ejecutamos (ab-1a-1b Y2)2. Con esto colocaremos uno o dos centros y dejaremos el cubo en uno de los casos ya vistos.
Esta tercera fase tiene 26 movimientos como máximo, y el método completo, 46.
Rodolfo Valeiras Reina, 11 de mayo de 2013.